(back to WP4)
Wavelet-based image assimilation operator:
divergence-free estimation and high-order regularization
Abstract
Expanding on a wavelet basis the solution of an image assimilation problem provides several advantages. Wavelet bases yield a natural and efficient multiresolution analysis frame work. The continuous representation of the solution with wavelets enables analytical calculation of regularization integrals over the spatial domain. By choosing differentiable wavelets, high-order derivative regularizers can be designed, either taking advantage of the wavelet differentiation properties or via the basis's mass and stiffness matrices.
Work in Progress
The wavelt-based optic-flow observation model is embedded in an image data assimilation procedure, in order to extract and analyze geophysical flows. In particular, numerical experiments based on the incompressible 2D Navier-Stokes model or on a simplified 3D model (Surface Quasi-Geostrophic model) are currently investigated.
References
1- S. Kadri-Harouna, P. Dérian, P. Héas, E. Mémin., Divergence-free Wavelets and High Order Regularization. Submitted.
2- P. Dérian, P. Héas, C. Herzet, E. Mémin., Wavelet-based fluid motion estimation. In Scale Space Methods and Variational Methods (SSVM) in Computer Vision, Israel, June 2011.
Some preliminary results:
Daubechies 3 (D3) stiffness matrix
Scaling function basis stiffness matrix of Laplacian operator (a) and corresponding wavelet basis (b): case of orthogonal Daubechies wavelet basis with 3 vanishing moments.
| (a) | 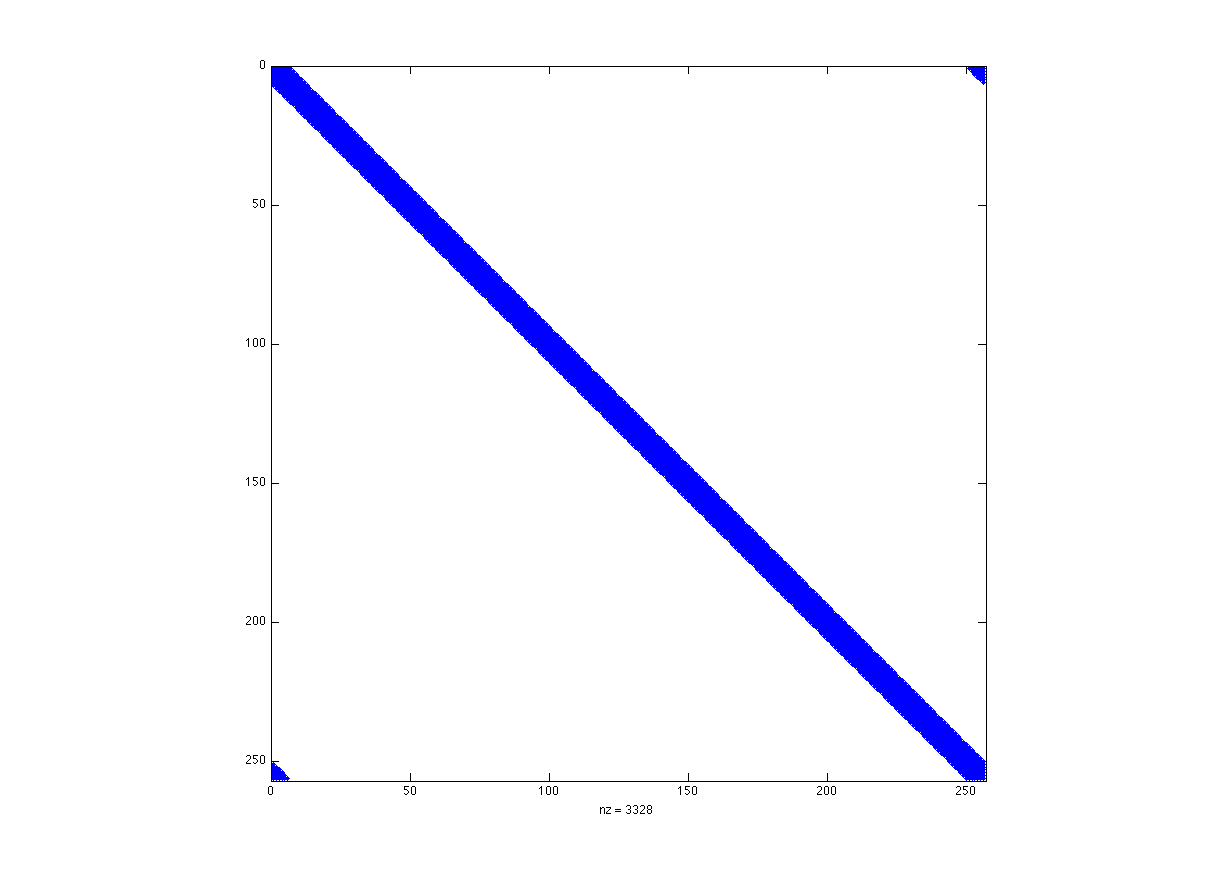 |
(b) | 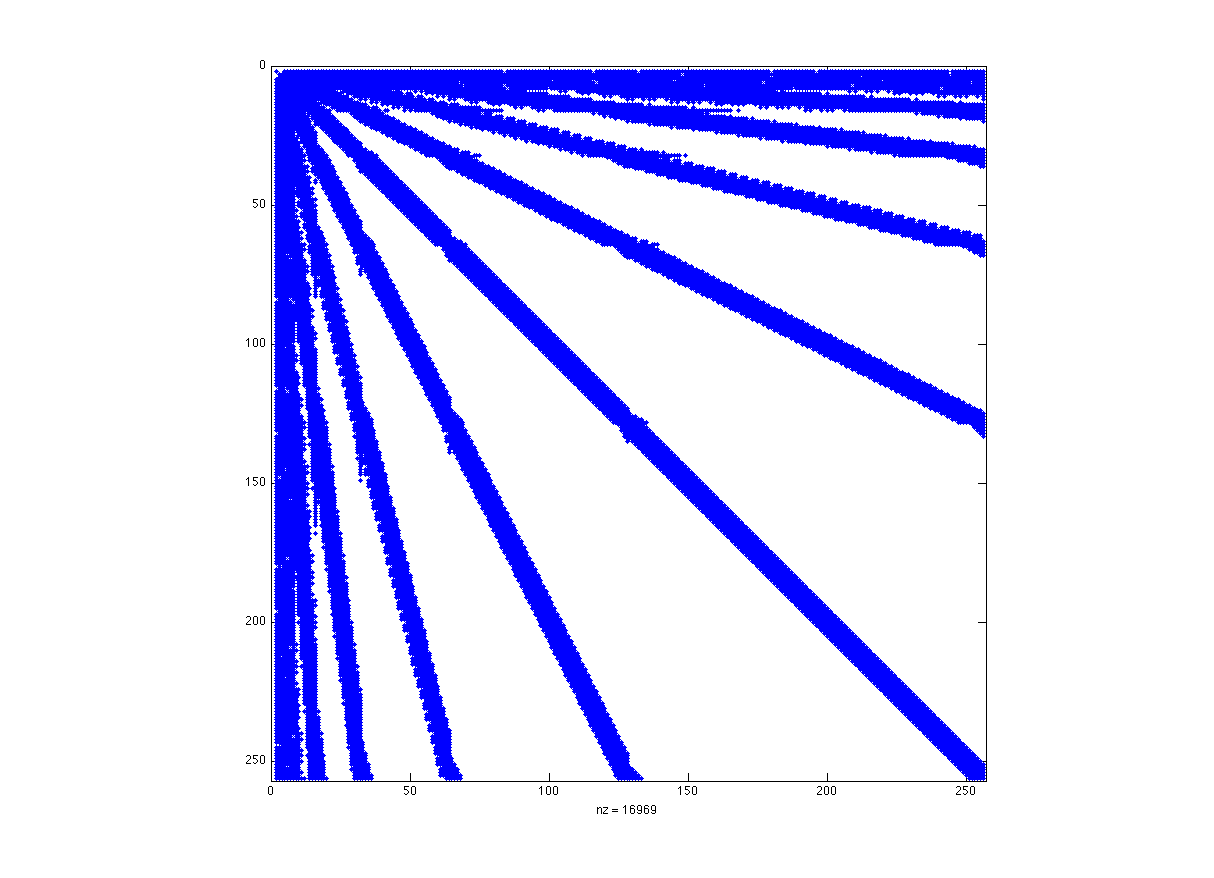 |
Synthetic sequence
Vorticity of estimated velocity field from two successive simulated particle images a fluid flow. The wavelet basis generator is Daubechies 7 (D7), using n=7 order derivative regularization.
Vorticity Estimated from Synthetic PIV Sequence
envoyé par pderian.
Kelvin-Helmholtz instability
The proposed method has been applied to a real sequence of 100 images (1024x1024 px), with a grad-curl regularization. Figures below show the vorticity field corresponding to motion estimated at two consecutive times (t=16 and t=17) and figure (e) represents the flow streamlines. Three different areas are visible: at the output of the jet (top of the field), shear regions begin to oscillate slowly. The middle region clearly shows the development of vortices characteristic of the Kelvin-Helmholtz instability. Finally, in the lower part of the field, structure of vortices collapse due to their tri-dimensionalization.
| (c) |  |
(d) | 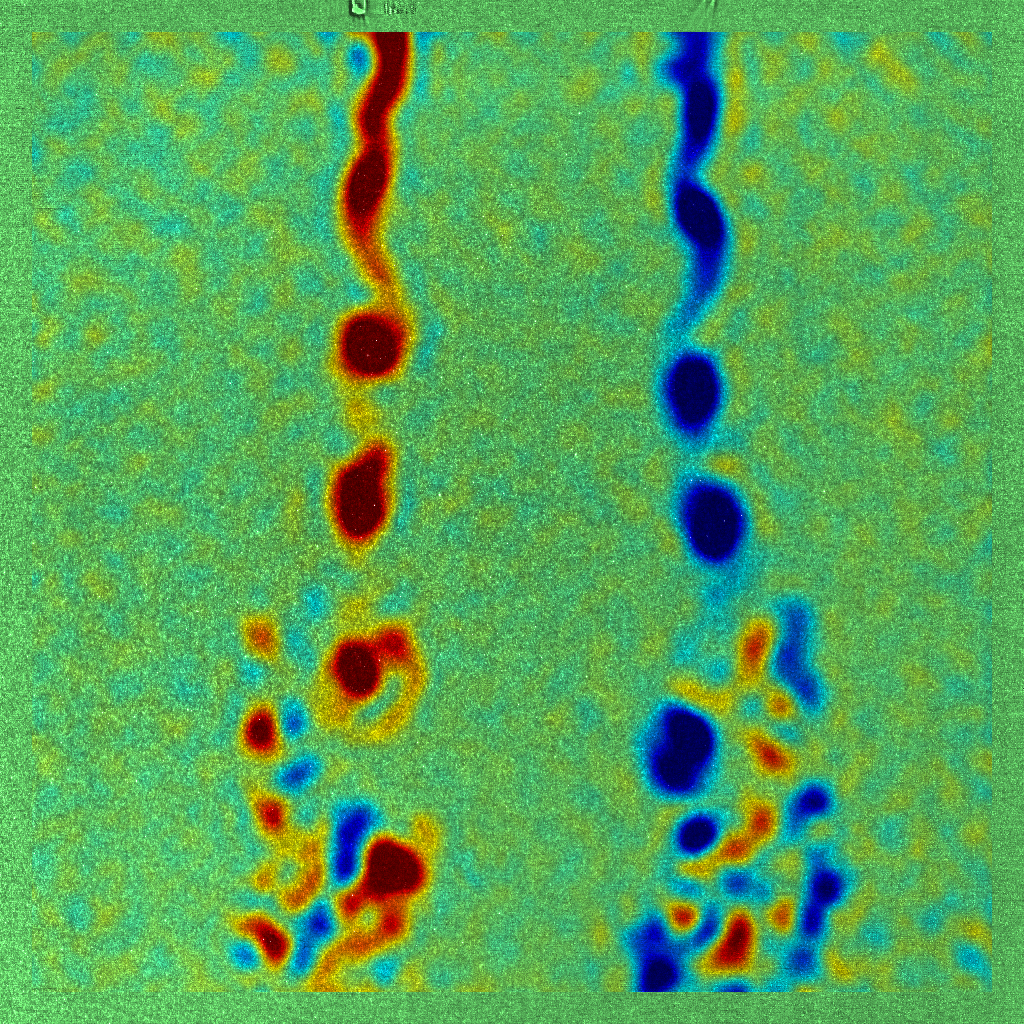 |
(e) |  |
Incompressible flows
Differential constraints on vector solutions, such as the divergence-free constraint in physics, can be handled with biorthogonal wavelet bases. In the particular case of motion estimation of incompressible flows, numerical results on synthetic and real images show that divergence-free wavelets and high-order regularizers are relevant.
Synthetic scalar images
The following figures show an input synthetic scalar image Fig. (f), the true vorticity Fig (g), the estimated vorticity Fig.(k) and the end-point error Fig. (i), where divergence-fee wavelet basis have been used with a Laplacian Regularization.
| (f) |  |
(g) | 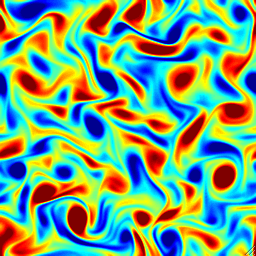 |
(h) | 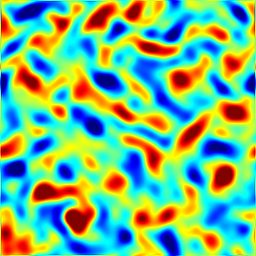 |
(i) |  |
Hereafter, in Fig. (j) and Fig. (k), we compare to state-of-the-art based on the end-point error.
| (j) | 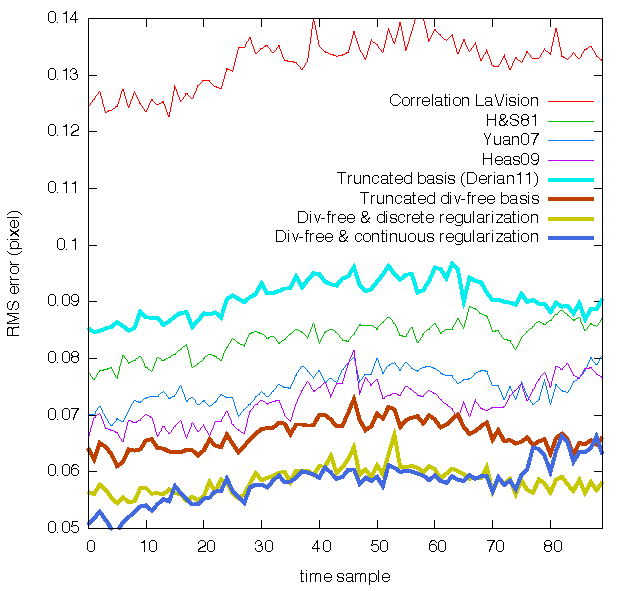 |
(k) | 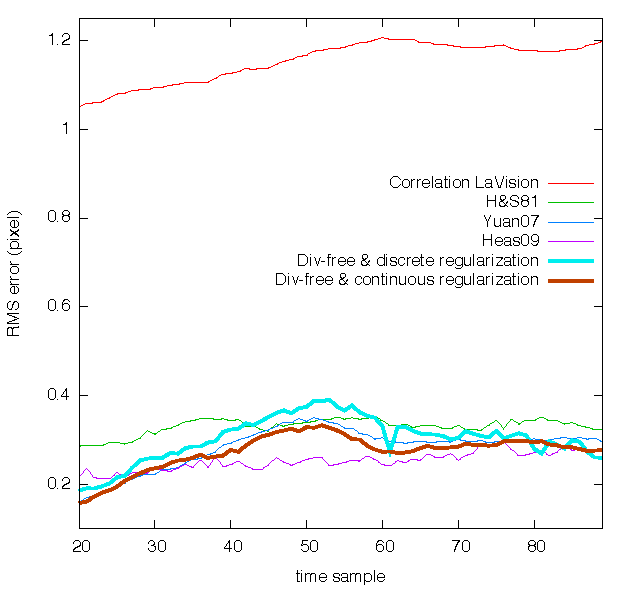 |
Real scalar images
Two consecutive vorticities estimated from a real scalar image sequence, using divergence-free wavelet basis and Laplacian regularization: input image Fig.(l), vorticity at t Fig. (m) and vorticity at t+1 Fig. (n).
| (l) | 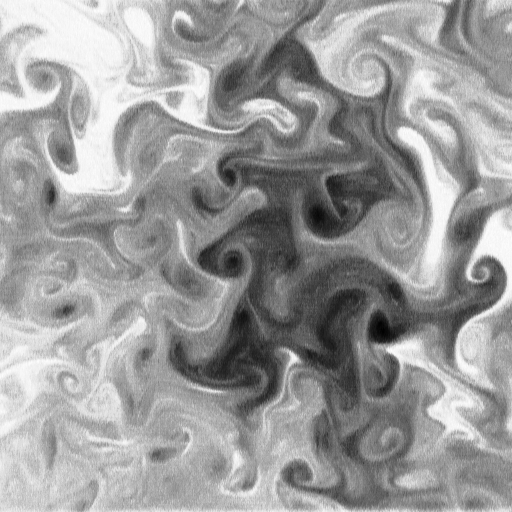 |
(m) | 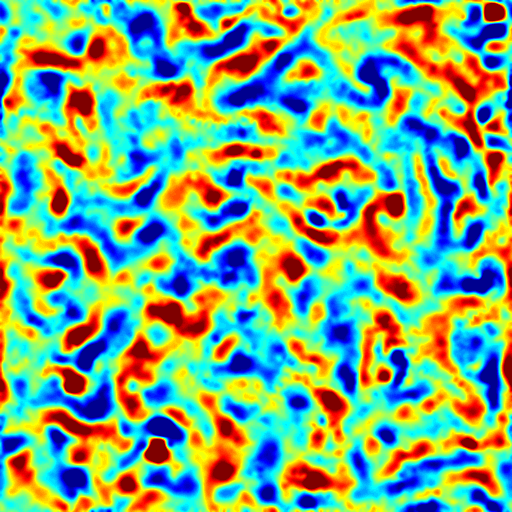 |
(n) |  |